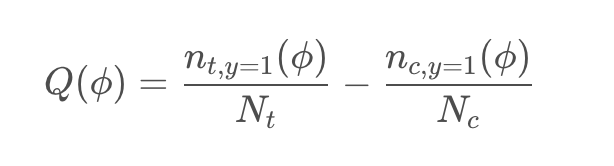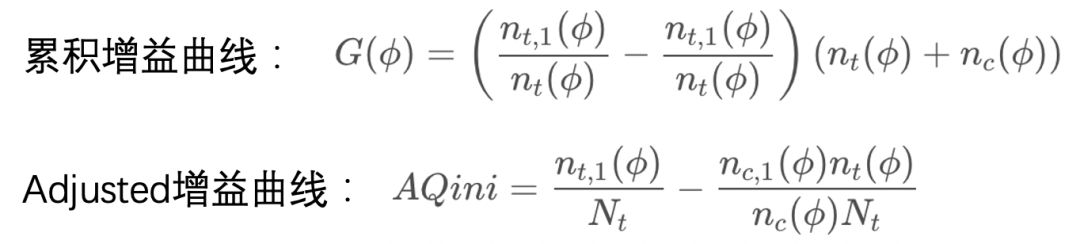一、什么是Uplift模型?
用一个简单的例子来介绍此模型。假设我们是个电商平台,一件标价300元的商品,用户的购买率为6%。现有一批预算可以给用户发放10元的优惠券以提升用户购买率。需要给每个用户都发放优惠券吗?答案显然是否定,那么这批优惠券应该发送给平台的哪些用户呢?
此时我们脑海中有四类用户:
- Persuadables:不发送优惠券则不买,发送优惠券则购买;
- Sure things:不论是否发送优惠券均会购买;
- Lost causes:不论是否发送优惠券均不会购买;
- Sleeping Dogs:不发送优惠券会购买,发送优惠券反而不买。
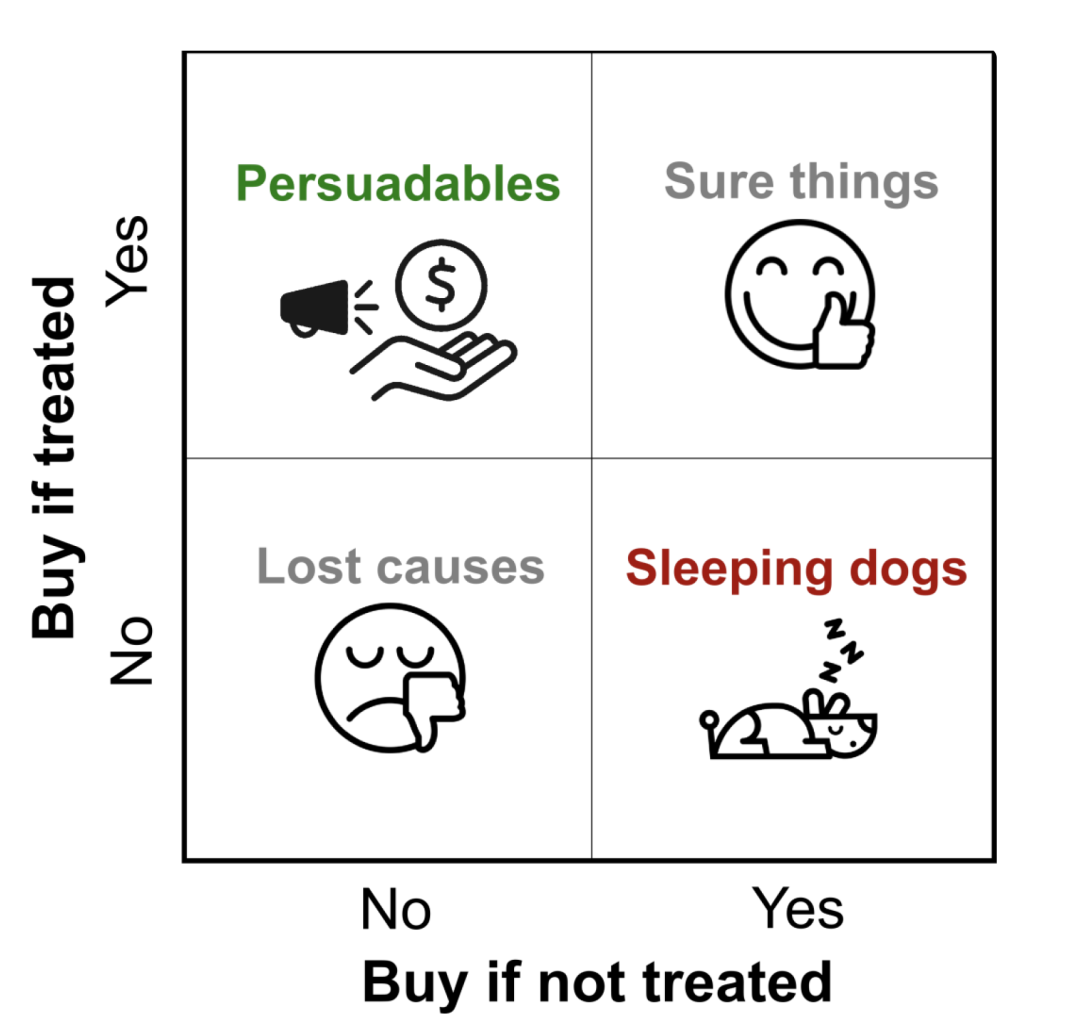
左上的Persuadables(说服型)类用户被发券后产生了正向变化,从不买转化为购买,干预后购买率得以提升,此部分是我们真正想要进行触达干预的营销敏感用户。
而右上的Surethings(确认型)类用户以及左下的Lostcauses(沉睡型)用户无论是否发券均不会改变其原本的购买行为,对这部分用户发送优惠券则会造成资源浪费。右下的SleepingDogs(勿扰型)用户对营销可能相对反感,干预会产生反效果,这类用户我们尽量避免打扰。
Uplift模型要解决的问题就是通过建模预测的方法精准的去对这四类用户进行分群。我们获取到的训练训练数据是不完整的,对于单个用户来说,不可能同时观测到在有干预(发券)和没有干预(不发券)两种情况下的表现,这也是因果推断中的反事实的问题。
可以从用户的角度来对平均因果效应做估计,假如我们有两组同质用户,对其中一组用户发券,另外一组不发券。之后统计这两群人在购买转化率上的差值,这个差值就可以被近似认为是可能的平均因果效应。
Uplift建模需要服从CIA条件独立假设,最简单的解决方式就是ab实验。因为样本在特征上分布较为一致,因此随机实验是Uplift Model建模过程中非常重要的前置条件。若随机实验下各个类别用户组数量性质较相似,则此Uplift模型即可较精准的预测给用户发放优惠券的收益。
首先,我们选取部分用户(小流量实验,样本量足够建模)随机分为实验组和对照组,对照组不发优惠券,实验组发放优惠券,用户最终是否购买为一个0-1变量;
然后,对整体实验数据用户购买行为进行建模;
最后,再用小流量实验训练得到模型对我们需要预测的全量用户进行条件平均处理效应估计,预测其发放优惠券所带来的增益值;
假设有N个用户,用户i在没有优惠券的购买结果为Yi(0),在有优惠券时购买结果为Yi(1),此时发送优惠券对该用户的增益就是uplift score (i)=Yi(1)-Yi(0)。当uplift score为正值时,说明干预项对用户有正向增益作用,也就是上文所提到的Persuadables(说服型)用户。
二、几种建模方法
1. Two-Learner
Two-Learner是基于双模型的差分模型,我们对实验组(有干预)和对照组(无干预)的购买行为进行分别建模,然后用训练所得两个模型分别对全量用户的购买行为进行预测,此时一个样本用户即可得出有干预和无干预情况下两个购买行为预测值。这两个预测值的差就是我们想要的uplift score。
这种建模方法较简单且易于理解,可以直接用回归、GBDT等模型实现。但也存在一些局限性:对照组和实验组分别建模,两个模型完全隔离,可能两个模型各有偏差从而导致预测的误差较大。其次建模的目标是Response而不直接是Uplift,因此模型对Uplift的预测能力较有限;策略只能是离散值,不能是连续变量,因为有几种策略就需要建几个模型。
所以当干预条件只有‘是否发优惠券’时,此建模方法可行,但是当涉及到‘多种优惠券面额/文案组合策略’或者‘发多大面额优惠券这种连续变量策略’时,本种建模方法可能并不非常work;
2. Single-Learner
Single-Learner在Two-Learner的基础上,将对照组数据和实验组数据放在一起建模,使用一个模型对处理效果进行估计,然后计算该样本用户进入实验组和对照组模型预测的差异作为对实验影响的估计。
与Two-Learner不同的是,本模型将实验分组(干预项)作为一个单独特征和其他变量一起放入模型中对用户购买行为进行建模,干预项可以是多种组合策略或者连续变量。
训练样本共用可以使此模型学习更加充分,通过单个模型的学习也可以避免双模型打分累积误差较大的问题。此外模型可以支持干预项为多策略及连续变量的建模,实用性较强。但此模型在本质上依然还是对Response建模,对Uplift的预测还是比较间接。
3. Class Transformation Method
Class Transformation Method模型既可以将实验组与对照组数据打通,同时它又是直接对Uplift score进行预测,计算用户在实验组中购买概率与在对照组中购买概率的差值,其核心思想是将实验组和控制组样本混合并创建新的变量z满足:
- 当用户在实验组(发券)且用户最终购买时,z=1
- 当用户在对照组(无干预)且用户最终未购买时,z=1
- 当用户在实验组(发券)且用户最终未购买时,z=0
- 当用户在对照组(无干预)且用户最终购买时,z=0
可以证明,P(Z=1│Xi)和Uplift Score是线性正相关的,且当实验组与控制组样本比例为1:1时,Uplift Score =2P(Z=1│Xi)-1,目标从预测UpliftScore转化为了预测P(Z=1│Xi)
三、Uplift模型评估
根据Uplift Score的定义,分数越高的用户即所谓的营销增益就越大。增益模型由于不能同时观测同用户在不同干预项下的真实增量,通常是通过划分十分位数来观测实验组用户和对照组用户样本来进行间接评估。
1. Uplift 十分位柱状图
将测试集预测出的用户按照Uplift Score由高到低平均分为10组,分别是top 10%用户,top 20%用户……top 100%用户。分别对每个十分位内的用户求实验组和对照组预测分数的均值,然后相减,计算不同分段中真正的实验提升收益。然后根据每个分组得出的实验收益,绘制十分位柱状图。这样,即可较直观观察到有多少的用户大概可以获得多少的营销增益。
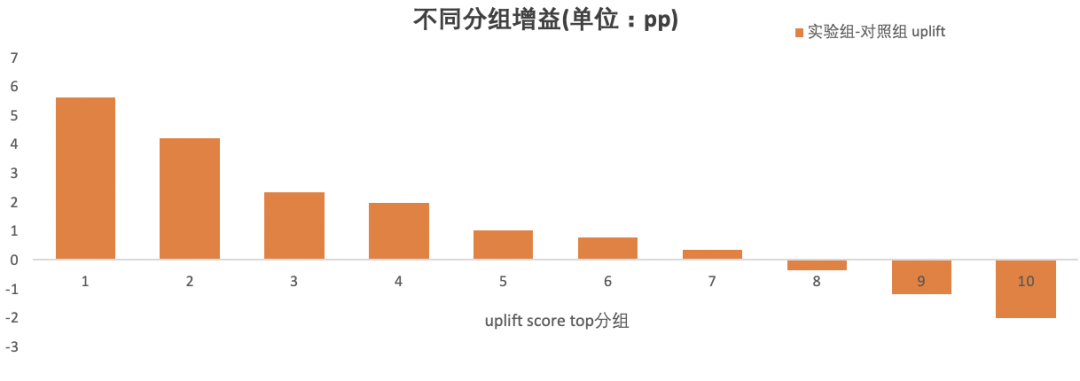
2. qini曲线(qini curve)
计算每组用户百分比的qini系数,将这些系数连接起来,得到一条qini曲线。qini系数公式如:
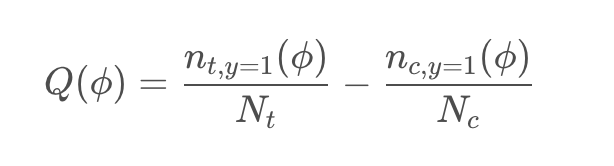
ϕ是按照Uplift Score由高到低排序的用户数量占实验组或对照组用户数量的比例,ϕ= 0.3即表示实验组或对照组中前30%的用户。nt,y=1(ϕ)表示在前百分比多少用户中,实验组中预测结果为购买的用户数量。nc,y=1(ϕ)表示在同样百分比用户中,对照组预测结果为购买的用户数量。Nt和Nc则分别代表实验组和对照组总用户样本数。
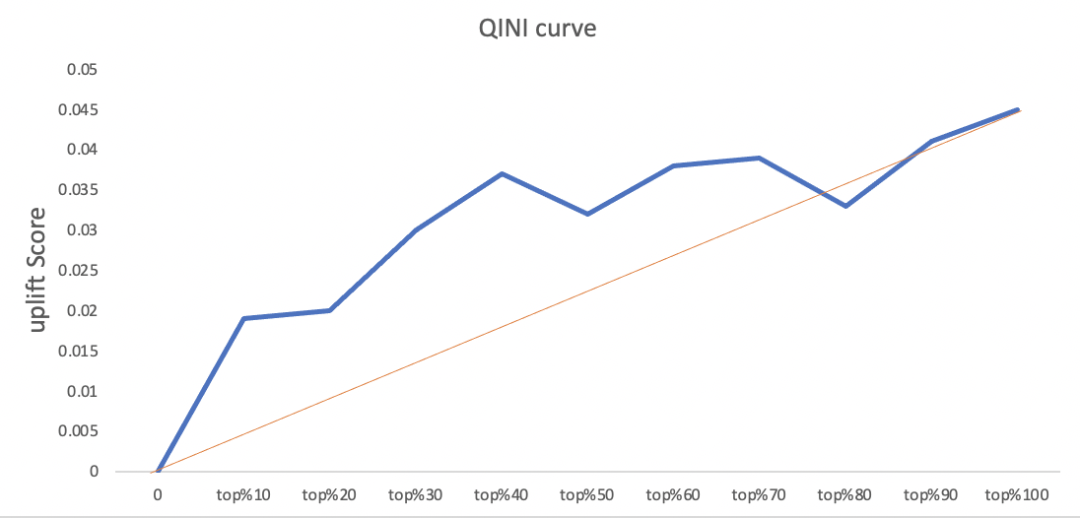
上图橙色线是随机曲线,qini曲线与随机曲线之间的面积作为评价模型的指标,面积越大表示模型结果远超过随机选择的结果。可以看到当横轴为top40%时,qini曲线与随机曲线之间距离最大,对应的纵轴大概是0.037,表示uplift score等于0.037可以覆盖前40%的用户数量,这部分用户也就是我们可以对其进行营销干预的persuadable用户。
但如果实验组和对照组用户数量不平衡,则会导致指标失真。另一种累积增益曲线可以避免这个问题。
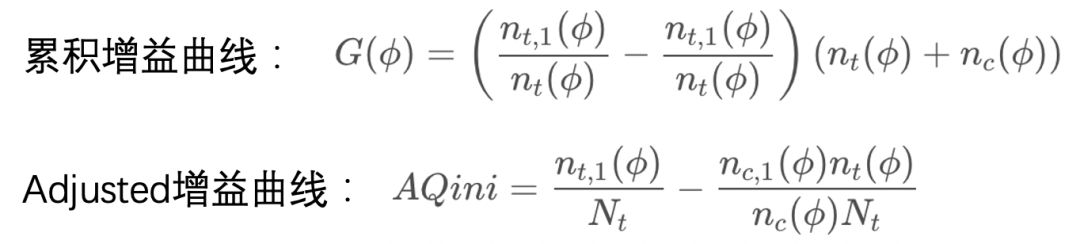
最后,我们总结一下Uplift模型可能的应用场景:
- 精准定位策略敏感人群:如全文所述,我们希望找出来一些对干预项(例如发券、投放等)比较敏感的用户,继而对其进行精准策略/营销;
- 测算收益空间:Uplift模型可以帮助我们测算如果对策略做一些人群向优化,业务收益将会提升多少;