前几天给孩子读田忌赛马,这是我们小时候都耳熟能详的一则寓言故事,当年只是知道哇塞一下孙膑的聪明、有谋略。老师也只是让总结一下故事结构、中心思想啥的,并没有深究孙膑是怎么想出这个法子的。如今回头来思考这则故事,发现其中蕴含的是一种典型的博弈思维,其意义远不是聪明那么简单。
孙膑,也许是他的天赋异禀让其可以脑袋一转就想出这么好的策略。但是,其背后隐藏的思维方式是不是可以总结出一套方法论?让我们这些没那么天赋异禀的普通人,今后在做事情的时候,也可以用这个方法论来做出科学正确的选择?
比如:一个互联网产品经理,经常需要应对接踵而至的各方需求,该如何科学地排列优先级呢?再比如:生活中如果碰到多项事情都需要解决,而我们的精力有限,该如何合理安排先做啥后做啥呢?
一、拆解孙膑的思维,梳理底层逻辑
梳理底层逻辑
话说田忌他们当时赛马时的规则是每方出上、中、下三等马各一匹,两两对阵赛三场,三局两胜。田忌的马总是比齐威王的马略逊,所以总是输。
孙膑在脑子一转,对这个事情做了一次全面复盘,把几种组合挨个对比,找出一条最优方案,于是取得了胜利。按现在的行话来说,这就是一次典型的博弈思维+降维打击。
咱脑子没孙膑好使,一时半会想不明白,老老实实地把所有可能的比赛组合都列出来看看:
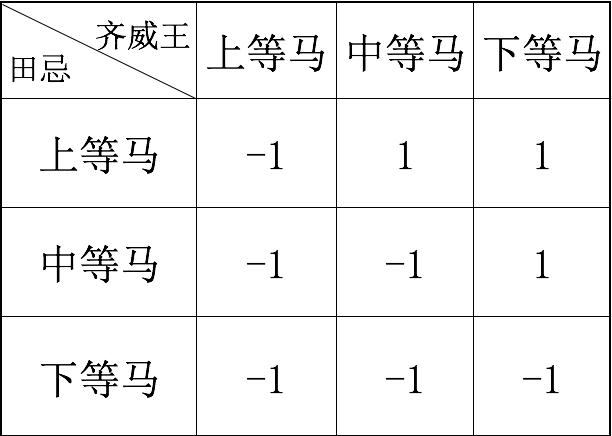
孙膑脑中的博弈模型
上图用一个博弈矩阵表示出所有对阵的胜负情况,1代表田忌赢,-1代表田忌输。从这个矩阵可以直观地得出如下结论:
- 面对齐威王的上等马,无论田忌出什么马都得输;
- 面对齐威王的中等马,田忌只有出上等马才能赢;
- 面对齐威王的下等马,田忌出上或中等马均能赢;
基于上述结论,只要是正常的普通人逻辑都可以简单得出孙膑的取胜之道:
- 反正都是输,索性多输点,用下等马和对方上等马比,后面必须赢两场;
- 只能用上等马和对方的中等马才能赢;
- 剩下中等马对阵对方的下等马,还是赢;
最终三局两胜,田忌胜!这也是唯一胜利的方案。
上述分解动作表明,孙膑的“神机妙算”其实也没啥高深的,分解下来普通人也一样可以得出必胜妙招,总结一下就是遇到问题三步走:
- 全面了解问题相关信息(如:田忌赛马的规则,失败原因等);
- 根据掌握的信息客观罗列出每一种策略及结果,构建相应的博弈矩阵;
- 在每一种可能性中,选出对最优的策略。
遇事三步走:“全面了解、客观罗列、选择最优”,这就是孙膑在田忌赛马事件中所用到的底层逻辑。
二、优先级评估模型,和孙膑一样做正确的选择
在日常的工作和生活中,我们经常会碰到各种事情、问题一起摆在面前有待解决,好像都很重要、都非常紧急。这时,如果没有通过一套合理科学的方法来选择做事情的优先次序,经常的情况就是,领导说啥急就先做啥(最终还是自己去背锅)或者自己一边做这件事的时候又去焦虑另外一件事情,结果两件事情都没有做好。
接下来,结合一个真实的工作场景,演示如何运用孙膑的思维来做正确的优先级评估:
小F是一家科技公司的产品经理,日常很重要的一个工作就是收集整理来自各方的需求,分析设计后,交付给研发团队进行研发排期。这些需求,有来自老板的、客户的、运营部的、自己根据行业趋势设计的等等多种渠道。每个需求方,都认为自己的需求最重要、最迫切,而研发资源又有限,小F该如何从海量的需求池里面,科学的选出最该做的10个功能呢?
按上述【遇事三步走】的方法:全面了解、客观罗列、选择最优。
1. 全面了解能掌握的需求信息
在这个场景下就是,定义清晰每一项需求,建立一张类似下图的表格:
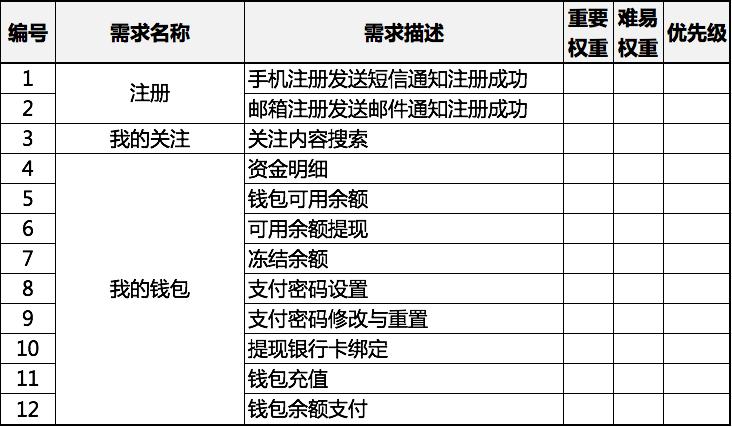
需求列表
这里省略掉一些其他的字段(比如:需求来源、分类、提出时间等),只保留了最重要的,我们把每一项需求的【优先级】,拆解成【重要权重】和【难易权重】这两项。为何要这样分拆?
因为,在一个软件系统的开发项目中,核心的矛盾就是有限的开发资源和无限的功能需求之间的矛盾,落实到具体的角色就是开发人员和需求提出方。为了高效地解决这个问题,就需要科学制定优先级。
所以,需要分别站在双方的角度来思考每一个功能点的重要性和难易度:需求提出方对自己提出的需求重要程度肯定是最有发言权的;开发人员对每一个功能的开发难度、完成周期是最清楚的。这两个维度将用于后面构建博弈矩阵来确定优先级。
2. 客观罗列每项需求的重要程度和难易程度
做好这一步,需要把重要权重和难易权重用具体的数值来量化:
- 【重要权重】分三级:1-2-3,数值越大越重要;
- 【难易权重】分三级:1-2-3,数值越大越简单;
这里说明一个容易混淆的地方,这两个维度指的是重要性和难易度对优先级的影响权重,并不完全是代表其本身的,所以,【难易权重】是越简单,对优先级的影响权重数值越大(生活中,我们通常的逻辑也是先易后难)。
定义好两个维度的量化数值规则后,就需要找到对应的责任人,分别来对每项功能进行客观的评估打分:
- 【重要权重】找需求提出者对所提出的需求项进行打分;
- 【难易权重】找研发人员(通常是组长)来各需求项打分;
打分后将各项得分填入上面的表格,如下图所示:
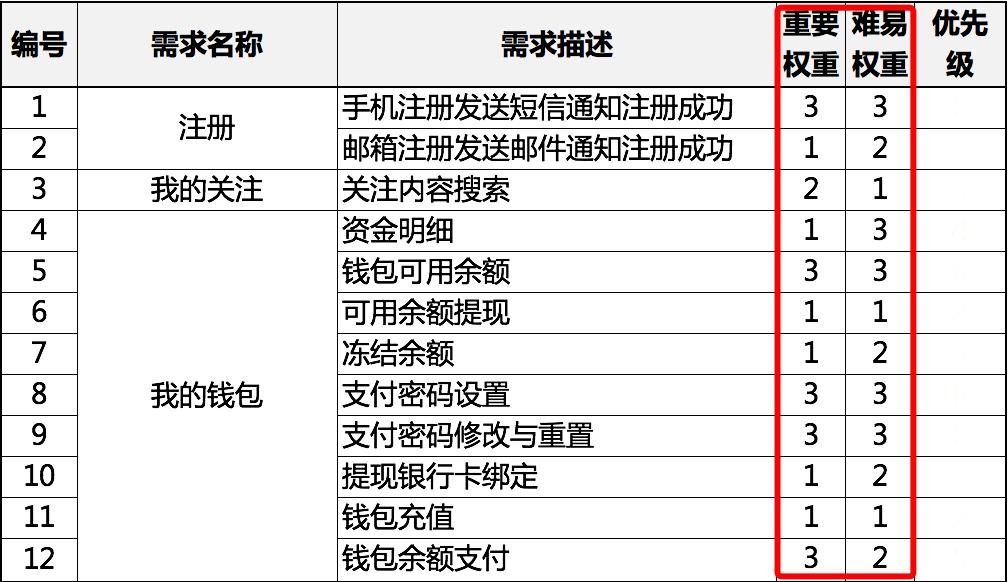
打分后的需求表
3. 构建博弈矩阵,选择最优的优先级排列
根据上一步的结果,我们以【重要权重】为纵坐标,【难易权重】为横坐标,就得到了一个二维的博弈矩阵,通过这个矩阵,可以很直观的展现出每一个功能点落在那个区域,先直接上图:
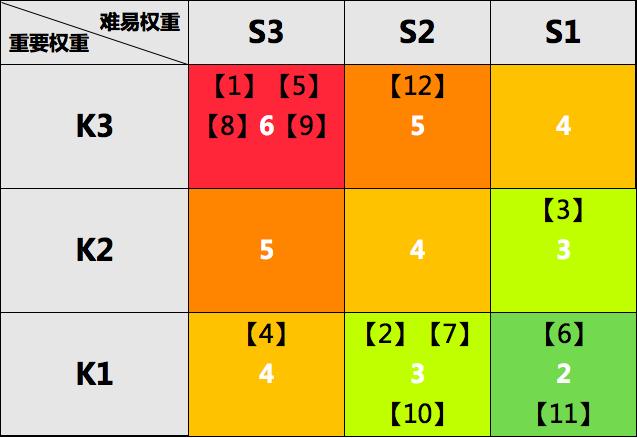
优先级博弈矩阵
这个矩阵中:
- 白色数字表示优先级数值,其等于该单元格对应的横纵坐标数值之和,数字越大就代表优先级越高;单纯从数值来说,可以分成5个优先级别,用红、橙、黄、黄绿、绿色标示;
- 【】方框内序号代表需求表里面每一项需求的序号,根据其重要权重和难易权重就可以确定其应该放入哪个区域块,其优先级数值就是两个权重数值之和。
比如:需求【1】其横纵坐标为(3,3),就应该放入6这个单元格,其优先级就是横纵坐标之和,说明这个功能又重要又容易完成,那肯定是先做这个需求是最合理的。
看到这个,大家肯定有疑问了,那如果两个功能的优先级数值都一样,都是3,但是在不同的区域块内,先做哪个呢?
用另一个例子说明:需求【3】和【2】,它们的优先级数值一样,但是【3】是在(2,1)这个区域块内,【2】是在(1,2)这个区域块内,数值虽然一样,但是背后代表的意义却不同。【3】(2,1)表示这个功能的重要权重要大于难易权重,而【2】(1,2)恰恰相反。
这种情况,要根据实际情况来定其最后的优先级:如果研发资源相对宽松时,就先做重要权重高的【3】;如果研发资源很紧缺了,就只能先做简单点的【2】。
大部分情况下,我们可以直接把两个维度的权重数值直接相加得到优先级数值,然后根据数值大小排序即可,如下图:
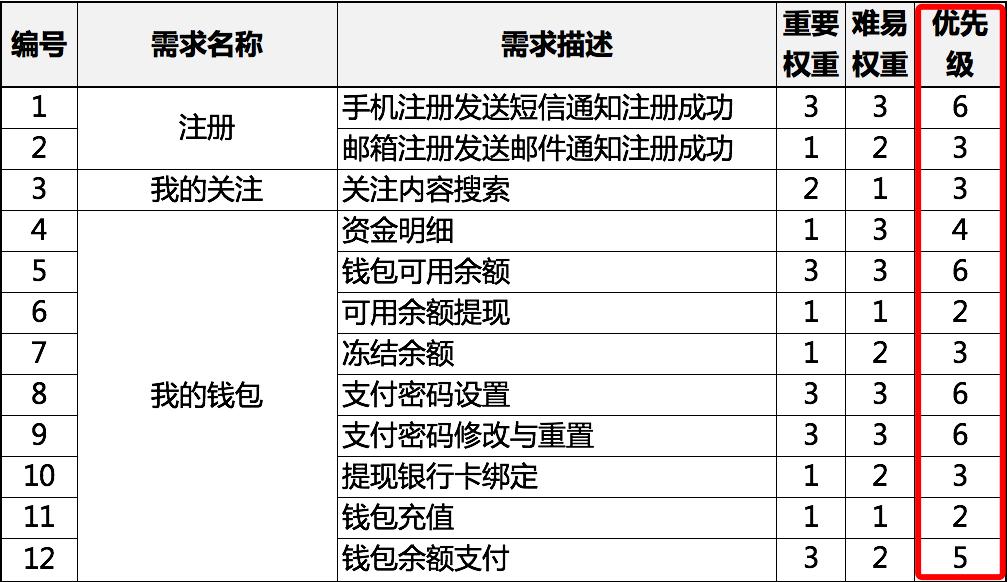
优先级数值
三、写在最后的话
其实,在生活中,我们也经常会碰到很多重要的事情一起出现的场景,比如:婚礼筹备、孩子备考、旅行安排等等。如果可以用遇事三步的这种逻辑,理性地分析一下,可以让我们做事情更加高效,减少焦虑。田忌赛马的故事给我们最大的启发不是孙膑的方案,而是孙膑思考出这个方案的逻辑。